Как определяется передаточное отношение. Передаточные отношения рядовых и многоступенчатых передач
При пересопряжении зубьев следующий зуб второго колеса должен попасть в следующую впадину первого, т.е. шаги на находящихся в зацеплении колес должны быть одинаковыми:
Таким образом, для одной пары колес прямо пропорционально отношению и обратно пропорционально отношению чисел зубьев колес, составляющих пару:
Знак передаточного отношения показывает направление вращения колеса на выходе по отношению к направлению вращения на входе:
- (+) – направления вращения на входе и на выходе совпадают. Для пары колес направление вращения совпадает при внутреннем зацеплении (рисунок 35б);
- (–) – колеса вращаются в противоположные стороны. Это происходит при внешнем зацеплении (рисунок 35а).
На рисунке 35 дана фронтальная проекция передач, а также их условное изображение на кинематических схемах при виде сбоку (или в разрезе).
Многоступенчатая передача
Для увеличения кинематического эффекта несколько зубчатых пар могут последовательно соединяться в единый . Такой механизм называется многоступенчатым зубчатым механизмом или многоступенчатой передачей . Схема одного из таких механизмов приведена на рисунке 36.
Рисунок 36
Запишем передаточные отношения для каждой пары колес данного механизма:
Из схемы видно, что колеса 2 и 3 находятся на одном валу и вращаются с одной угловой скоростью (ω 2 = ω 3 ), аналогично ω 4 = ω 5 . Поэтому в приведенном выше уравнении эти члены сократились.
Таким образом, общее передаточное отношение многоступенчатого механизма равно произведению частных передаточных отношений ступеней, из которых состоит данный механизм:
В этой формуле “m” – число передач внешнего зацепления (если число передач внешнего зацепления четное, то знак "+", т.е. колеса на входе и на выходе вращаются в одну сторону; если нечетное, то знак "–". Количество передач внутреннего зацепления не учитывается, т.к. внутреннее зацепление не изменяет направление вращения).
В приведенном примере m=2 (пары Z 1* Z 2 и Z 3* Z 4 ; пара Z 5* Z 6 – пара внутреннего зацепления) и, таким образом, колеса "1" и "6" вращаются в одну сторону.
Планетарные и дифференциальные механизмы
В практике применяются зубчатые механизмы, имеющие колеса с подвижными геометрическими осями (сателлиты ). Такие механизмы называются планетарными (если имеют одну ) или дифференциальными (если степень свободы равна двум).
Планетарные и дифференциальные механизмы позволяют получить более высокий кинематический эффект, более высокий , более удобную компоновку. Дифференциальные механизмы позволяют также раскладывать одно движение на два или складывать два движения в одно.
Рисунок 37
На рисунке 37 приведен пример дифференциального (рисунок 37 а) и планетарного механизмов (рисунок 37 б). В этих механизмах колесо "2" имеет подвижную геометрическую ось – это и есть сателлит.
Неподвижная геометрическая ось, вокруг которой движется ось сателлита, называется центральной осью . Колеса, геометрические оси которых совпадают с центральной, также называются центральными (на рисунке 37 колеса "1" и "3" – иногда такие колеса называют солнечными). , соединяющее ось сателлитов с центральной осью, называется водилом (водило обычно обозначается "H").
Записываем уравнение передаточного отношения между центральными колесами этого многоступенчатого механизма (для того, чтобы отличить передаточное отношение механизма с остановленным водилом от первоначально заданного, в верхнем индексе ставят обозначение водила H. Для данного примера читается – передаточное отношение от первого к третьему при остановленном водиле):
Формулу такого типа, полученную на основе метода обращения движения, называют формулой Виллиса. В данном конкретном механизме (рисунок 38) имеется еще одна особенность – колесо 2 входит последовательно в два зацепления (с первым и третьим колесами), являясь ведомым для первого колеса и ведущим – для второго.
Полученная формула является универсальной для обоих механизмов, изображенных на рисунке 37. Дифференциальный механизм, изображенный на рисунке 37а, имеет две степени свободы, а поэтому для определенности движения надо задать законы движения двум звеньям. При этом возможны следующие варианты:
- заданы ω 1 и ω 3 ; из записанной формулы определяется ω H (вариант, изображенный на рисунке 37 а);
- заданы ω 1 и ω H ; из записанной формулы определяется ω 3 ;
- заданы ω H и ω 3 ; из записанной формулы определяется ω 1 .
Так как звеньям можно задавать любые законы движения, то, как частный случай, одному из центральных колес зададим угловую скорость, равную нулю. Например, в рассматриваемом механизме зададим ω 3 =0 , другим словами, затормозим третье колесо. Таким приемом отнимается одна из двух степеней свободы, и механизм из дифференциального превращается в планетарный (рисунок 37 б).
Таким образом, планетарный механизм это частный случай дифференциального, когда одно из центральных колес неподвижно (заторможено).
Поэтому решаются эти механизмы совершенно одинаково, по одним и тем же уравнениям, только в планетарном механизме для неподвижного колеса в уравнение подставляется значение угловой скорости, равное нулю. Для изображенного на рисунке 37б планетарного механизма:
Деление передач на рядовые и ступенчатые имеет смысл, когда они содержат более двух подвижных звеньев. На рис. 17, а ,б показаны примеры рядовой и ступенчатой передач, соответственно.
Колёса рядовой передачи располагаются в одной плоскости или, иначе, в один ряд, отсюда и происходит название. В ступенчатой передаче каждая пара зацепляющихся колёс располагается в своей плоскости, образует свою ступень. На виде б) :1 ,2 - первая ступень; 3, 4 - вторая.
В рядовой передаче каждое звено содержит только одно зубчатое колесо. Номер звена и номер колеса совпадают. В ступенчатой передаче колёса 2 и3 располагаются на одной ступени (одном валу), поэтому иногда они обозначаются номером вала, на котором они располагаются, и различаются по индексу, например 2′, 2′′ или 2а, 2б. Номер звена не проставляется, так как содержится в обозначениях колёс.
Рядовая и ступенчатая передачи образуют класс передач с неподвижными осями колёс . Для любой такой передачи передаточное отношение от первого звена к последнему,n -му,равно произведению промежуточных передаточных отношений. Это правило выражается формулой
u1,n = u1,2u2,3... un-1,n , (12)
где индексы указывают номера звеньев. Для доказательства справедливости формулы представим каждое u в виде отношения скоростей:
ω1 = ω1ω2 Lωn −1 .
ωn ω2ω3ωn
После сокращений уравнение обращается в тождество, что и доказывает справедливость формулы (12). Формула справедлива для любой последовательной цепи механизмов. При этом uij (здесь и далее запятую опускаем) есть передаточное отношение отдельного механизма.
Применим формулу (12) к передачам, изображённым выше. Для рядовой передачи
| u =u u u | z | 2 | − | z | 3 | − | z | 4 | =− | z | 4 | . | ||||||
| = | − | |||||||||||||||||
| z | z | z | ||||||||||||||||
| 14 12 23 | 34 | 2 | 3 | z | ||||||||||||||
| 1 | 1 |
Для ступенчатой передачи
| z2 ′ | z3 | z2 ′z3 | |||||||||
| u =u u = | − | − | = | . | |||||||
| z | z | ||||||||||
| 13 12 23 | z z | ||||||||||
| 1 | 2 ′′ | 1 2 ′′ |
Результаты показывают, что передаточное отношение рядовой передачи зависит от чисел зубьев только крайних колёс. Ступенчатая передача не обладает таким свойством. Знак «минус» в передаточном отношении u14 показывает, что колёса1 ,4 вращаются в разные стороны.
11. Дифференциальные и планетарные передачи. Формула Виллиса.
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами.
Планетарные механизмы подразделяются на планетарные редукторы и мультипликаторы, которые обладают одной степенью свободы и обязательно имеют опорное звено, и зубчатые дифференциальные механизмы, число степеней свободы которых два и более, и которые опорного звена обычно не имеют.
К типовым планетарным механизмам относятся:
· однорядный планетарный механизм со смешанным зацеплением (механизм Джеймса);
· двухрядный планетарный механизм со смешанным зацеплением;
· двухрядный планетарный механизм с двумя внешними зацеплениями;
· двухрядный планетарный механизм с двумя внутренними зацеплениями.
Элементы планетарного механизма имеют специальные названия:
· зубчатое колесо с внешними зубьями, расположенное в центре механизма называется "солнечным";
· колесо с внутренними зубьями называют "короной" или "эпициклом";
· колеса, оси которых подвижны, называют "сателлитами";
· подвижное звено, на котором установлены сателлиты, называют «водило». Это звено принято обозначать не цифрой, а латинской буквой h.
При вращении солнечного колеса сателлиты поворачиваются как рычаг относительно мгновенного центра вращения (опорное колесо неподвижно) и заставляют вращаться водило. При этом планетарные колеса (сателлиты) совершают сложное движение: вращаются вокруг собственной оси (относительно водила) с угловой скоростью и вместе с водилом обкатываются вокруг его оси (переносное движение). Число степеней свободы этого механизма равно единице. Поэтому редуктор имеет постоянное передаточное отношение.
Обычно у реального механизма имеется несколько симметрично расположенных блоков сателлитов . Их вводят с целью уменьшения габаритов механизма, снижения усилия в зацеплении, разгрузки подшипников центральных колес, улучшения уравновешивания водила, хотя механизм в этом случае имеет избыточные связи, т.е. является статически неопределимым. При кинематических расчетах учитывается один сателлит, так как остальные являются пассивными в кинематическом отношении.
Если в рассмотренном механизме освободить от закрепления опорное колесо (корпус редуктора) и сообщить ему вращение, то все центральные колеса станут подвижными и механизм превратится в дифференциальный, так как число степеней свободы его будет равно двум.
Таким образом, дифференциальный механизм – это планетарный механизм с числом степеней свободы .
Число степеней свободы (подвижности) механизма показывает, скольким звеньям дифференциала необходимо сообщить независимые движения, чтобы получить определенность движения всех остальных звеньев. Здесь в зависимости от направления вращения наружных валов может происходить либо разложение движения (одного ведущего на два ведомых), либо сложение движения. Ведущим считается такой вал, у которого направление скорости вращения и момента совпадают. Следовательно, планетарный редуктор (или мультипликатор), имеющий неподвижное колесо, можно превратить в дифференциал, если освободить неподвижное (опорное) колесо и сообщить ему вращение. Наоборот, любой дифференциал можно превратить в планетарный редуктор, если закрепить одно (при W = 2) или несколько из его центральных колес. Это так называемое свойство обратимости планетарных механизмов, которое позволяет применять одинаковые методы исследования и проектирования для редукторов и для дифференциалов. При этом каждому элементарному дифференциалу будут соответствовать два планетарных редуктора
В таблице приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.
Типовые планетарные механизмы
| № | Структурная схема механизма | Uред | КПД |
| 3....10 | 0.97....0.99 | ||
 | 7....16 | 0.96....0.98 | |
| 25....30 | 0.9....0.3 | ||
 | 30....300 | 0.9....0.3 |
Формула Виллиса
Формула Виллиса выводится на основании основной теоремы зацепления и устанавливает соотношение между угловыми скоростями зубчатых колес в планетарном механизме. Рассмотрим простейший планетарный механизм с одним внешним и одним внутренним зацеплением. Всему механизму сообщается угловая скорость равная по величине и противоположна по направлению угловой скорости водила, при этом водило остановится, а опорное колесо начнет поворачиваться. Таким образом, планетарный механизм превратится в механизм с неподвижными осями, состоящий из нескольких последовательно соединенных зубчатых колес. Такой механизм носит название обращенного механизма.
Угловые скорости звеньев в каждом из рассматриваемых движений приведены в таблице
В движении звеньев относительно водила угловые скорости звеньев равны угловым скоростям в движении относительно стойки минус угловая скорость водила. Если в движении относительно стойки ось сателлита подвижна, то в движении относительно водила оси обоих зубчатых колес неподвижны. Поэтому к движению относительно водила можно применить основную теорему зацепления.
Передаточное отношение обращенного механизма 
, окончательно передаточное отношение планетарного редуктора может быть определено по формуле Виллиса:
Передаточное отношение планетарного редуктора от любого колеса к водилу равно единице минус передаточное отношение обращенного механизма от этого колеса к опорному.
Государственное образовательное учреждение высшего
профессионального образования
НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Кафедра «Теоретическая механика»
ЗУБЧАТЫЙ МЕХАНИЗМ
Методические указания к курсовому проекту
По теории механизмов и машин
Нижний Новгород 2005Составитель: Б.Ф.Балеев, А.Н.Гущин
УДК 621.01/075/
Зубчатый механизм: Методические указания к курсовому проекту по теории механизмов и машин / НГТУ; Сост.: Б.Ф.Балеев, А.Н.Гущин. – Н.Новгород, 2005. – 31 с.
Научный редактор А.Ю.Панов
Подп. в печать. Формат 60х84 1 / 16 . Бумага газетная. Печать офсетная.
Печ. л. Уч.-изд. л. Тираж экз. Заказ
Нижегородский государственный технический университет.
Типография НГТУ, 603600, ул. Минина, 24
© Нижегородский государственный
Технический университет, 2005
1. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МНОГОЗВЕННЫХ
ЗУБЧАТЫХ МЕХАНИЗМОВ
Кинематический анализ зубчатых передач с неподвижными осями заключается в определении их передаточных отношений при известных числах зубьев зубчатых колес.
На рис.1 показана пара зацепляющихся зубчатых колес (изображены только начальные окружности). Передаточное отношение от первого зубчатого колеса ко второму i 12 по определению равно:
.
| а) | б) |
Рис.1. К определению передаточного отношения зубчатой передачи
Знак «минус» показывает, что направления угловых скоростей ведущего и ведомого колес противоположны. Точка II – полюс зацепления (мгновенный центр относительных скоростей). Скорость полюса выражается через угловые скорости зубчатых колес ω 1 и ω 2 , радиусы начальных окружностей r w 1 и r w 2:
,
откуда
.
(1)
Числа зубьев колес пропорциональны их начальным радиусам
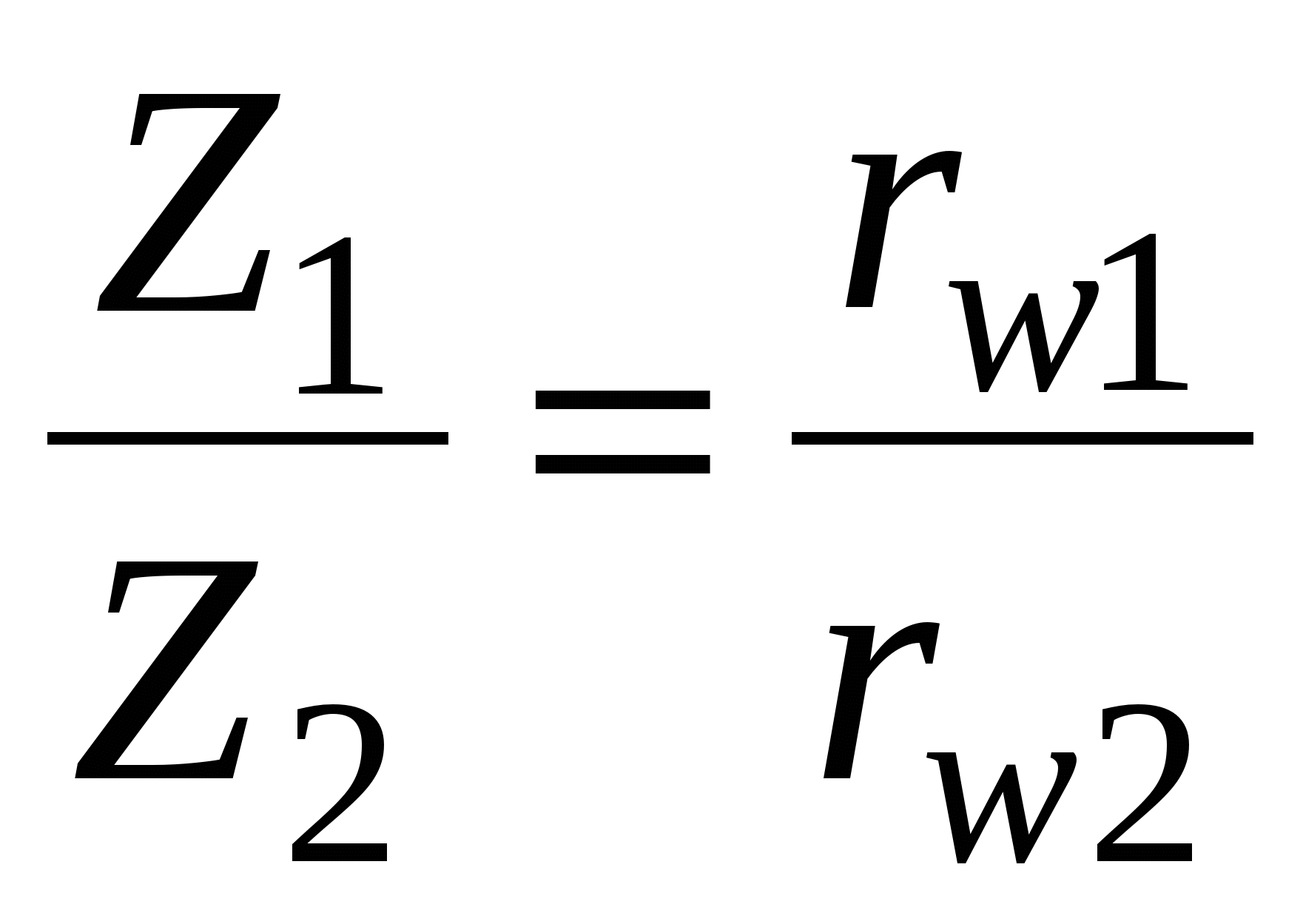, поэтому передаточное отношение
.
Для внутреннего зацепления пары колес (рис.1, б
) передаточное отношение – величина положительная, так как направление угловых скоростей ведущего и ведомого колес совпадают.Если имеется n зацепляющихся зубчатых колес (мгновенный механизм, рис.2), то передаточное отношение находится как произведение передаточных отношений каждой ступени:
. (2)
где k – число внешних зацеплений. Внутренние зацепления не учитываются, так как они не меняют знака.
Рис.2. К определению передаточного отношения многозвенного зубчатого механизма
Пример
Определить передаточное отношение механизма, изображенного на рис.3. Числа зубьев колес равны: Z
1 = 28, Z
2 = 54, 
= 18, Z
3 = 60, 
= 20, Z
4 = 50,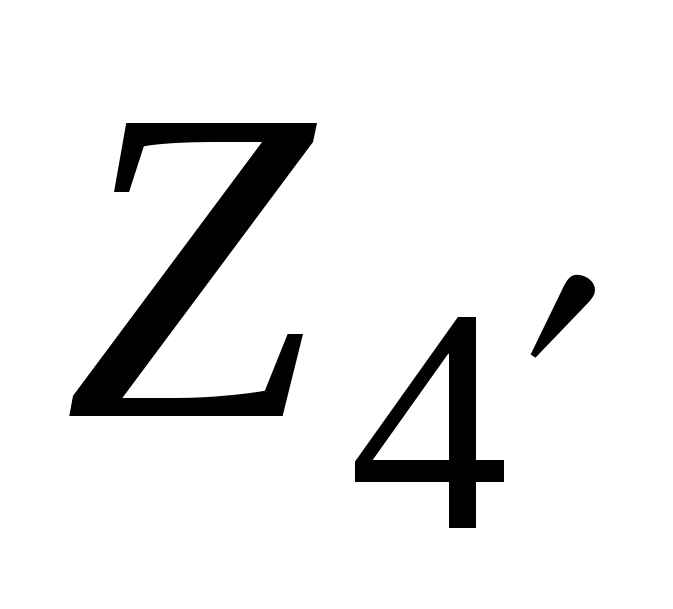 
= 18, Z
5 = 45, 
= 17, Z
6 = 80.
Рис.3. Многозвенный зубчатый механизм
2. СИНТЕЗ МНОГОЗВЕННОГО ЗУБЧАТОГО МЕХАНИЗМА
Кинематический синтез зубчатых механизмов заключается в распределении (разбивке) общего передаточного отношения по ступеням и определении чисел зубьев колес.
Поставленные задачи можно решить лишь для конкретного механизма, учитывая предъявляемые к нему требования, которые, в свою очередь, зависят от многих факторов, таких как, характер нагружения, требуемая надежность и долговечность механизма, условия взаимозаменяемости, условия смазки, охлаждения, ограничения шума и вибрации и т.п. Как видно, поставленные задачи можно решить, рассматривая одновременно геометрические, кинематические, динамические, технологические, прочностные и другие параметры и факторы.
Таким образом, не может быть общих рекомендаций разбивки передаточного отношения любого механизма по ступеням.
Числа зубьев зацепляющихся колес определяются требуемой плавностью зацепления, допускаемыми габаритами передачи, модулем зубьев. Модули вычисляются в результате расчета зубьев на прочность.
Как правило проектирование начинается с предварительных расчетов и компоновки механизма, когда многие параметры назначаются ориентировочно, опираясь на данные практики. Затем проводится полный расчет, полученные величины корректируются, и выполняется проверочный расчет. Методика полного расчета зубчатых механизмов будет излагаться в курсе «Детали машин».
Рассмотрим решение поставленных задач на примере двухступенчатого редуктора. Установлено, что габариты и масса редуктора существенно зависят от распределения передаточного отношения по ступеням, а лучшие показатели имеют редукторы, у которых диаметры ведомых колес обоих ступеней приблизительно одинаковы. В этом случае обеспечивается смазка погружением колес в общую масляную ванну.
В силовых механизмах (предназначенных для передачи и преобразования крутящего момента) рекомендуется для одной ступени цилиндрической зубчатой передачи назначать передаточное отношение не ниже 8, а для конической – не более 5. Это связано с тем, что при i > 8 целесообразно выполнить редуктор двухступенчатым, так как габариты и масса его будут существенно меньше, чем у одноступенчатого с тем же передаточным отношением.
В кинематических механизмах часто главными требованиями являются: точность воспроизведения заданных функций механизма, ограничение величины мертвого хода и т.п., поэтому при проектировании их руководствуются иными требованиями по сравнению с силовыми механизмами. Прочностные показатели зубчатых колес таких механизмов часто не рассматриваются.
В зубчатых редукторах силы, действующие на зубья каждой последующей ступени, больше сил в зацеплении предыдущей ступени, поэтому модуль зубьев второй ступени, как правило, больше модуля зубьев первой ступени. При незначительной разнице в расчетных значениях модулей их часто принимают одинаковыми, что упрощает и удешевляет изготовление зубчатых колес и улучшает условия взаимозаменяемости. В кинематических механизмах модули всех колес часто одинаковы.
Числа зубьев зацепляющихся колес должны быть выбраны так, чтобы отсутствовало подрезание, заострение и интерференция зубьев, а при высоких скоростях их суммарное число следует брать большим, чем при низких скоростях, так как при больших числах зубьев увеличивается коэффициент перекрытия и, следовательно, улучшается плавность зацепления.
Передаточное отношение первой ступени обычно больше передаточного отношения второй ступени, так как т 2 больше т 1 . Это обусловлено получением приблизительно одинаковых размеров ведомых колес первой и второй ступеней, поскольку при этом обеспечивается лучшая, по сравнению с другими вариантами, компоновка двухступенчатого редуктора и условие смазки зубчатых колес (рис.4, 5).
Рис.4. Схема двухступенчатого редуктора с общим передаточным отношением i i 12 = 4,4, второй – i 23 = 3,39
Рис.5. Схема двухступенчатого редуктора с общим передаточным отношением i 13 = 15; передаточное отношение первой ступени i 23 = 3,87 и равно передаточному отношению второй ступени
Следует заметить, что подобные рекомендации не могут быть приемлемы для любого механизма. Например, в трансмиссиях транспортных машин желательно наибольшее передаточное отношение иметь на последней ступени, чтобы разгрузить всю предыдущую цепь звеньев от больших передаваемых крутящих моментов, что позволяет снизить размеры и массы деталей.
Пример 1
Определить числа зубьев колес двухступенчатого редуктора (рис.6), у которого общее передаточное отношение i 13 = 15, модуль зубьев первой ступени т 1 т 2 = 1,5 мм.
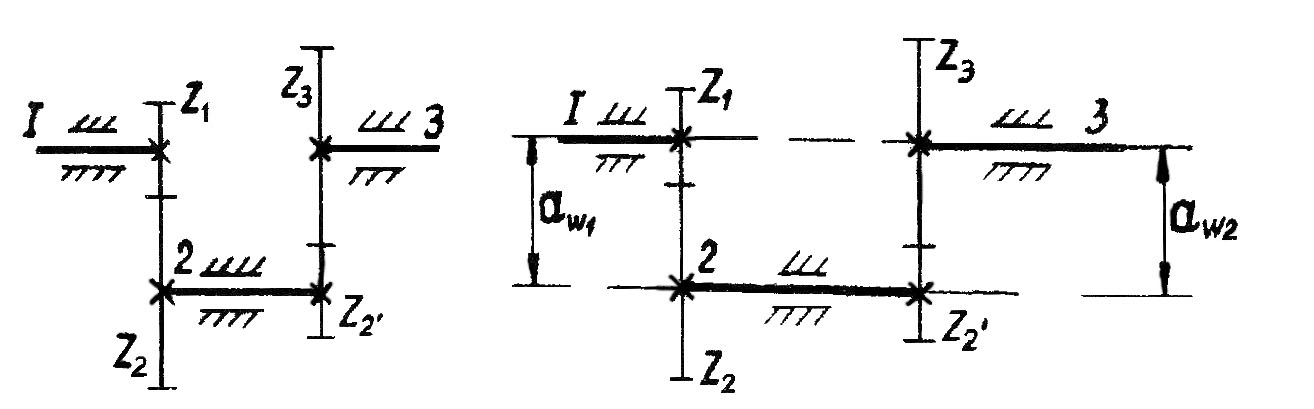
Рис.6. Схема двухступенчатого редуктора
Для кинематического расчета редуктора известно лишь общее передаточное отношение. Модули определяются в расчете зубьев на прочность, поэтому они приняты известными, чтобы иметь возможность закончить кинематический расчет.
В решении поставленной задачи нет необходимости учитывать, со смещением нарезаны колеса или без смещения, так как это обстоятельство учитывается при расчете зубьев на прочность. Несколько иные размеры колес смещенной передачи непосредственно не влияют на передаточное отношение, если числа зубьев колес смещенной и несмещенной передач одинаковы.
Общее передаточное отношение разбиваем по ступеням:
,
где i 12 – передаточное отношение первой ступени; i 23 – передаточное отношение второй ступени.
Для получения приблизительно одинаковых размеров ведомых колес каждой ступени примем передаточное отношение первой ступени несколько большим передаточного отношения второй ступени. Пусть i 12 будет больше i 23 в 1,3 раза, тогда
i
12
= 1,3 i
23
или 
.
Теперь можно найти передаточное отношение второй ступени i 23:
.
Определим передаточное отношение первой ступени:
Числом зубьев колеса Z 1 следует задаться. Для этого необходимо знать некоторые параметры, влияние которых изучается в курсе деталей машин (требования к плавности зацепления, предполагаемая долговечность, материал зубчатого колеса и т.п.). Примем Z 1 = 20 – несколько больше Z min и определим число зубьев колеса Z 2:
Диаметр колеса Z 3 должен быть несколько больше колеса Z 2 ввиду того, что при почти одинаковых размерах ведомых колес первой и второй ступеней и модулях, отличающихся в 1,5 раза, число зубьев колеса может оказаться меньше минимального. Поэтому примем d 3 = 1,1 d 2 , где d 2,3 – диаметры делительных окружностей.
Определим d 2: d 2 = m 1 Z 2 = 1 88 = 88 мм.
Найдем d 3: d 3 = 1,1 d 2 = 1,1 88 = 96,8 мм.
Определим число зубьев колеса Z 3:
.
Округлим Z 3 до целого числа: Z 3 = 65.
Теперь получим число зубьев колеса :
Округляем до целого числа: = 19.
Найдем передаточное отношение механизма с вычисленными значениями чисел зубьев колес:
Относительная погрешность передаточного отношения:
Диаметры делительных окружностей зубчатых колес:
Пример 2
Определить числа зубьев колес двухступенчатого соосного редуктора (рис.7). Модуль зубьев первой ступени т 1 = 1 мм, модуль зубьев второй ступени т 2 = 1,5 мм, общее передаточное отношение i 13 = 15.
Рис.7. Схема соосного двухступенчатого редуктора
Условие соосности требует равенства межосевых расстояний a w 1 и a w 2:
Выразим 
через
и передаточные отношения i
12
и i
23:
.
При равных передаточных отношениях ступеней очевидно, что 
, а следовательно, и r
w
2 =
r
w
3 .
Выразим межосевые расстояния через модули и числа зубьев колес первой и второй ступеней для несмещенных передач:
или
т.е.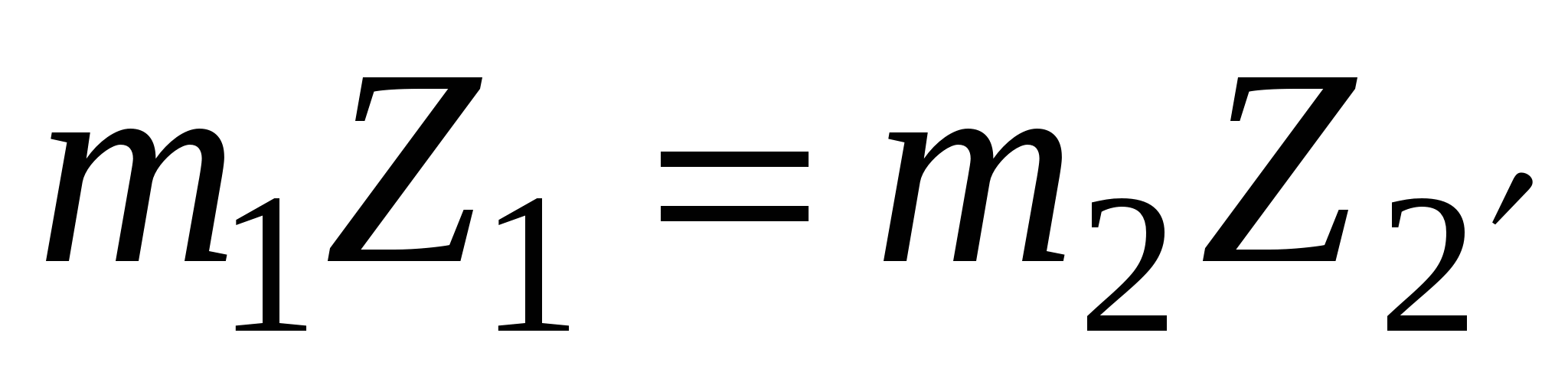 
, а так как m
1 = 1, а m
2 = 1,5, то 
.
Числом зубьев наименьшего колеса
следует задаться. Желая получить наименьшие габариты редуктора и имея ввиду, что вторая ступень тихоходная, преем 
– минимальному числу зубьев без подреза, нарезанных реечным инструментом без смещения.
Числа зубьев других колес станут равными:
Округлим Z 1 , Z 2 , Z 3 до целых чисел: Z 1 = 26, Z 2 = 101, Z 3 = 66.
Определим межосевые расстояния a 1 и a 2 , считая передачу несмещенной (a w = a ):
Определим полученное общее передаточное отношение:
Погрешность передаточного отношения:
Межосевые расстояния a w (мм) цилиндрических передач редукторов рекомендуется выбирать из следующих рядов:
1-ый предпочтительный ряд: 40, 50, 63, 80, 100, 125, 160, 200, 250, 313, 400, 500, 630, 800, 1000, 1250, 1600, 2000, 2500;
2-ой предпочтительный ряд: 140, 180, 225, 280, 355, 450, 560, 710, 900, 1120, 1400, 1800, 2240 (мм)
Ближайшее к расчетным значение межосевого расстояния – 63 мм. Чтобы привести межосевые расстояния обеих ступеней к выбранному значению a w = 63 мм, можно нарезать зубья одного из колес каждой ступени (при значительной разнице в расчетных и требуемых значениях – обоих колес) со смещением режущего инструмента. У первой ступени следует уменьшить межосевое расстояние на 0,5 мм, а у второй увеличить на 0,75 мм. Суммарный коэффициент смещения определяют по формуле:
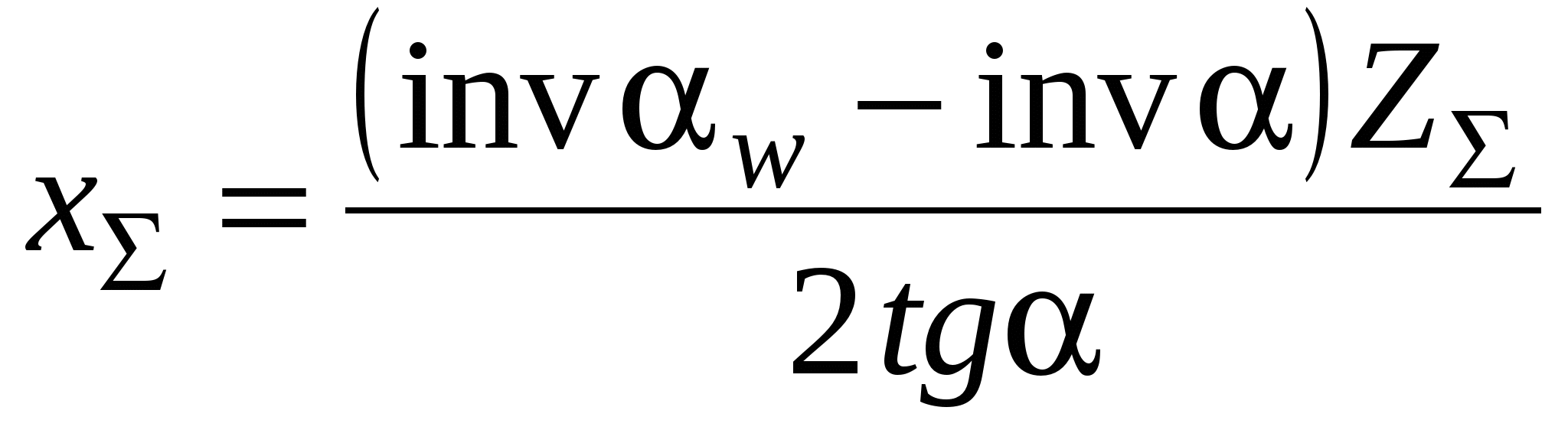. (3)
Углы зацепления α w 1 и α w 2 первой и второй ступеней находятся из известного соотношения:
для первой ступени получим: , где a 1 = 63,5 мм, α = 20º, a w 1 = a w = 63 мм
Для второй ступени: , где a 2 = 62,25 мм, a w 2 = a w = 63 мм, α = 20º
Инволюты углов α, α w 1 , α w 2 находится в таблицах эвольвентных функций по известным углам α = 20º, α w 1 = 18º40, α w 2 = 21º40.
inv 20º = 0,014904; inv 18º40 = 0,012038; inv 21º40 = 0,019120.
Определяем суммарный коэффициент смещения первой и второй ступеней x 1 и x 2 :
Примем x
1
= 0 и x
3
= 0, тогда x
1Σ
=
x
2
, а x
2Σ
= 
.
Необходимое смещение режущего инструмента:
для первой ступени b 1 = x 1 Σ m 1 = –0,499975 1= –0,5 мм;
для второй ступени b 2 = x 2 Σ m 1 = 0,480670 1,5 = 0,721 мм.
Другой способ «вписывания» передачи в заданное межосевое расстояние – с помощью косозубых колес подбором угла наклона зубьев.
В рассматриваемом примере в первой ступени придется оставить смещенную передачу, так как межосевое расстояние несмещенной передачи больше рекомендуемого и его необходимо уменьшить, а при нарезании косозубых колес их размеры увеличиваются при том же стандартном модуле т п . Вторую ступень выполним косозубой, чтобы показать метод определения наклона зубьев, хотя практически косозубой делают первую ступень, поскольку здесь большие, чем во второй ступени, окружные скорости колес, а косозубая передача обеспечивает лучшую плавность зацепления, которая необходима при высоких скоростях.
Геометрические параметры косозубого колеса, как известно, определяется по торцовому модулю, поэтому найдем его величину из условия равенства межосевого расстояния второй ступени рекомендуемому значению a w = 63 мм:
Известно, что 
, где β – угол наклона зубьев к оси колеса, а т
– нормальный модуль из числа стандартных, поэтому
.
3. ПЛАНЕТАРНЫЕ МЕХАНИЗМЫ
Кинематический анализ планетарных и дифференциальных механизмов (дифференциалов) заключается в определении передаточных отношений и угловых скоростей звеньев аналитическими и графическими методами.
В планетарных механизмах и замкнутых дифференциалах, как имеющих одну степень свободы, определяются передаточные отношения, а в дифференциалах находится связь между угловыми скоростями звеньев.
Метод определения передаточного отношения планетарного механизма, имеющего подвижные геометрические оси сателлитов, заключается в том, что этот механизм преобразуется в механизм с неподвижными геометрическими осями всех зубчатых колес (обращений), который и используется для определения искомого передаточного отношения.
Для получения обращенного механизма применяется метод обращения движения : всем звеньям механизма, включая стойку, сообщается угловая скорость водила. Водило останавливается, геометрические оси всех колес становятся неподвижными, а сами зубчатые колеса приобретают дополнительные угловые скорости. Относительные движения звеньев при этом не изменяются.
Сообщим всем звеньям дифференциала (рис.10) угловую скорость – ω в. Зубчатые колеса и Z 4 в дифференциал не входят, так как предоставляют простую зубчатую передачу. Скорости звеньев механизма станут равными:
Угловая скорость стойки – ω в;
Угловая скорость водила В –
;
Угловая скорость звена 1 – 
;
Угловая скорость звена 2 – 
;
Угловая скорость звена 3 –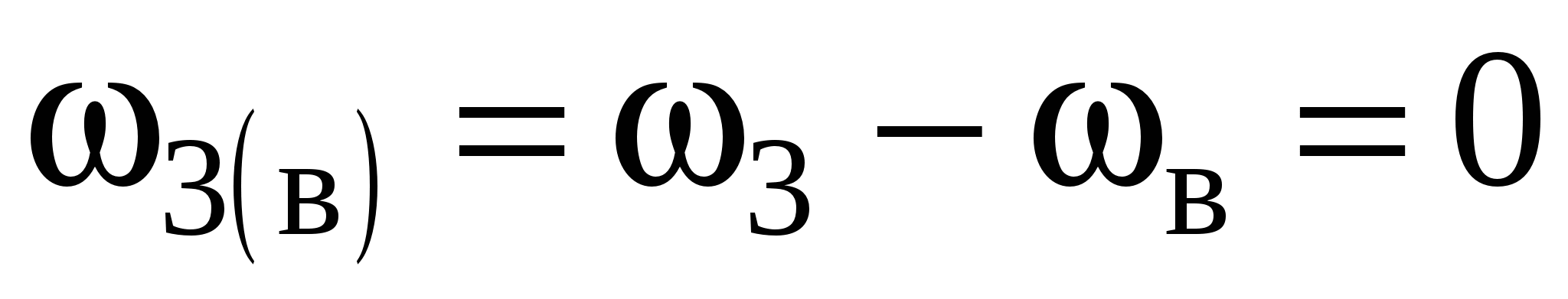 
.
Индекс в скобках указывает неподвижное звено.
В обращенном механизме может быть определено передаточное отношение между любыми звеньями. Например, передаточное отношение от звена 3 к звену 1 при неподвижном водиле
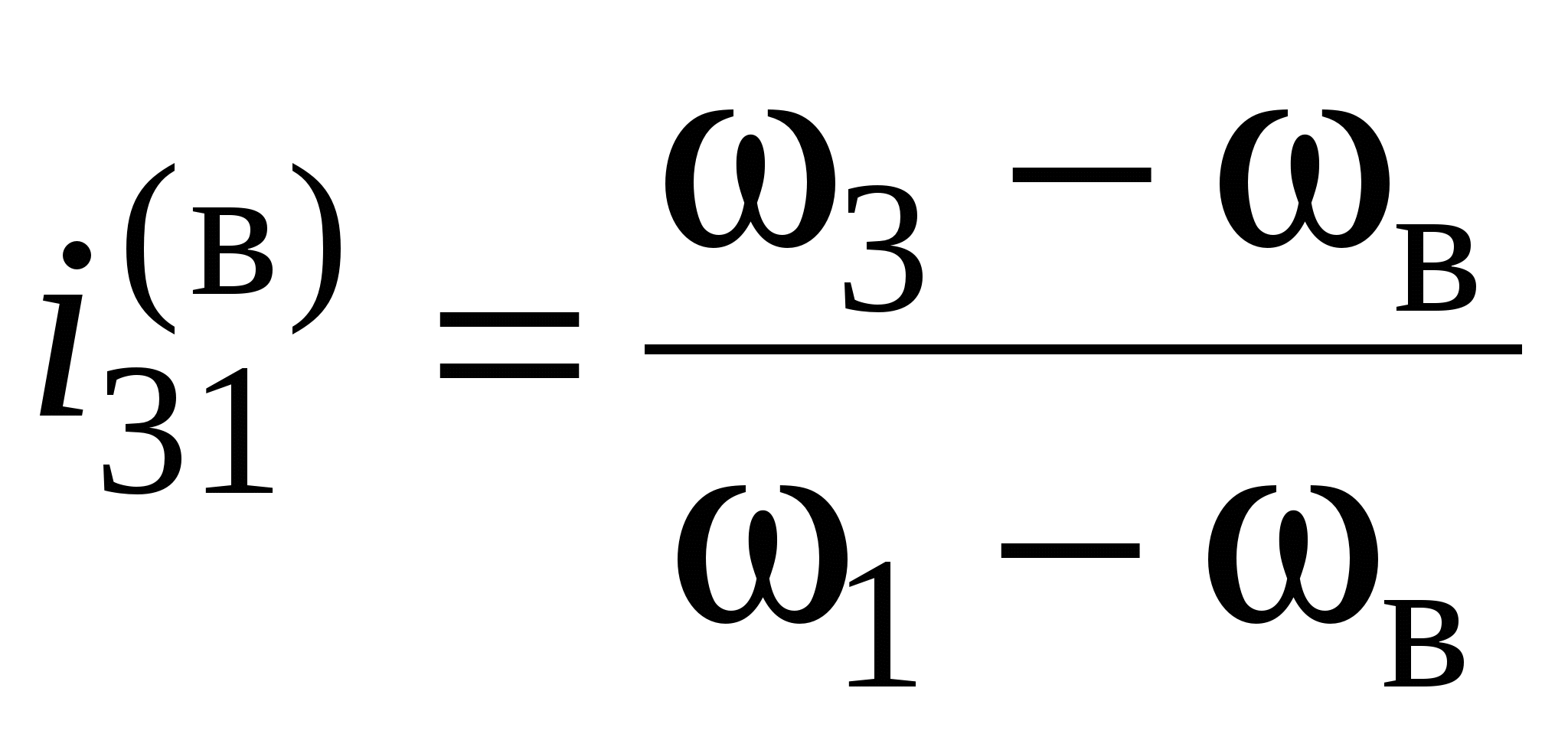(4)
– формула Виллиса для дифференциалов с двумя степенями свободы .
При любом числе звеньев формула Виллиса имеет вид
, (5)
где обозначения в индексе показывают звенья, между которыми определяется передаточное отношение. Например, 
читается так: передаточное отношение от звена «а» к звену «в» при неподвижном звене «с».
Если у дифференциала (рис.10) остановить звено 1, то механизм станет планетарным (рис.8). Зубчатые колеса и Z 4 составляют простую зубчатую передачу и в планетарный механизм не входят. Для обращенного планетарного механизма передаточное отношение может быть получено из формулы Виллиса для дифференциалов, если положить ω 1 = 0:
Индекс в скобках (1) показывает, что передаточное отношение определяется при неподвижном звене 1. Полученная зависимость позволяет найти передаточное отношение между звеньями механизма с подвижным водилом:
(6)
– формула Виллиса для планетарных механизмов.
В более общем виде при любом числе звеньев эта формула записывается так:
,
т.е. передаточное отношение от любого центрального колеса к водилу равно единице минус передаточное отношение обращенного механизма.
При определении передаточного отношения 
используется очевидное равенство 
и формула Виллиса для планетарных механизмов:
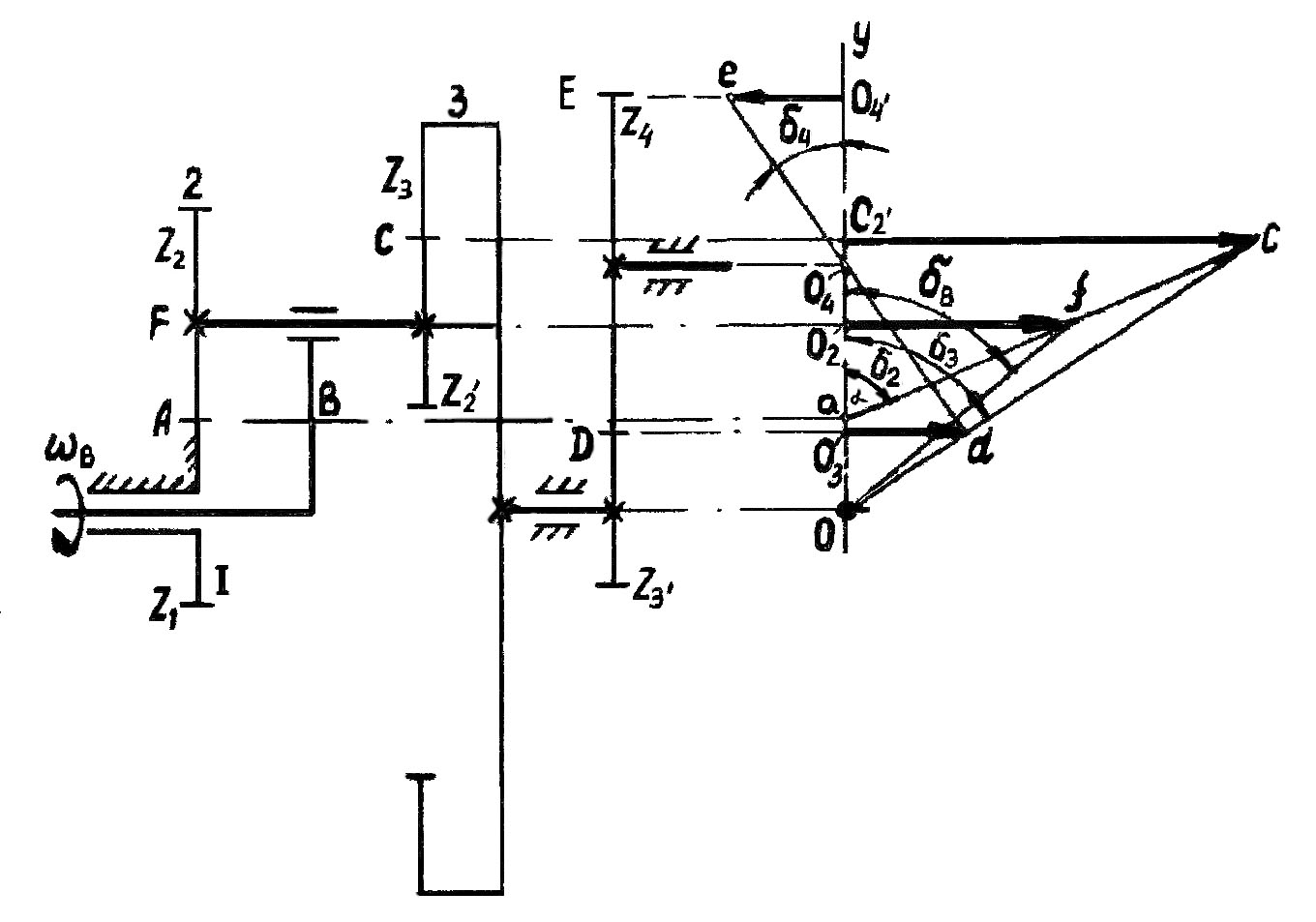
Рис.8. Схема и план скоростей планетарного механизма
В дифференциальном механизме координата одного из звеньев является функцией обобщенных координат звеньев, движения которых независимы:
.
Дифференцируя φ n как сложную функцию, получим:
где 
, 
, 
, 
, 
, 
, 
.
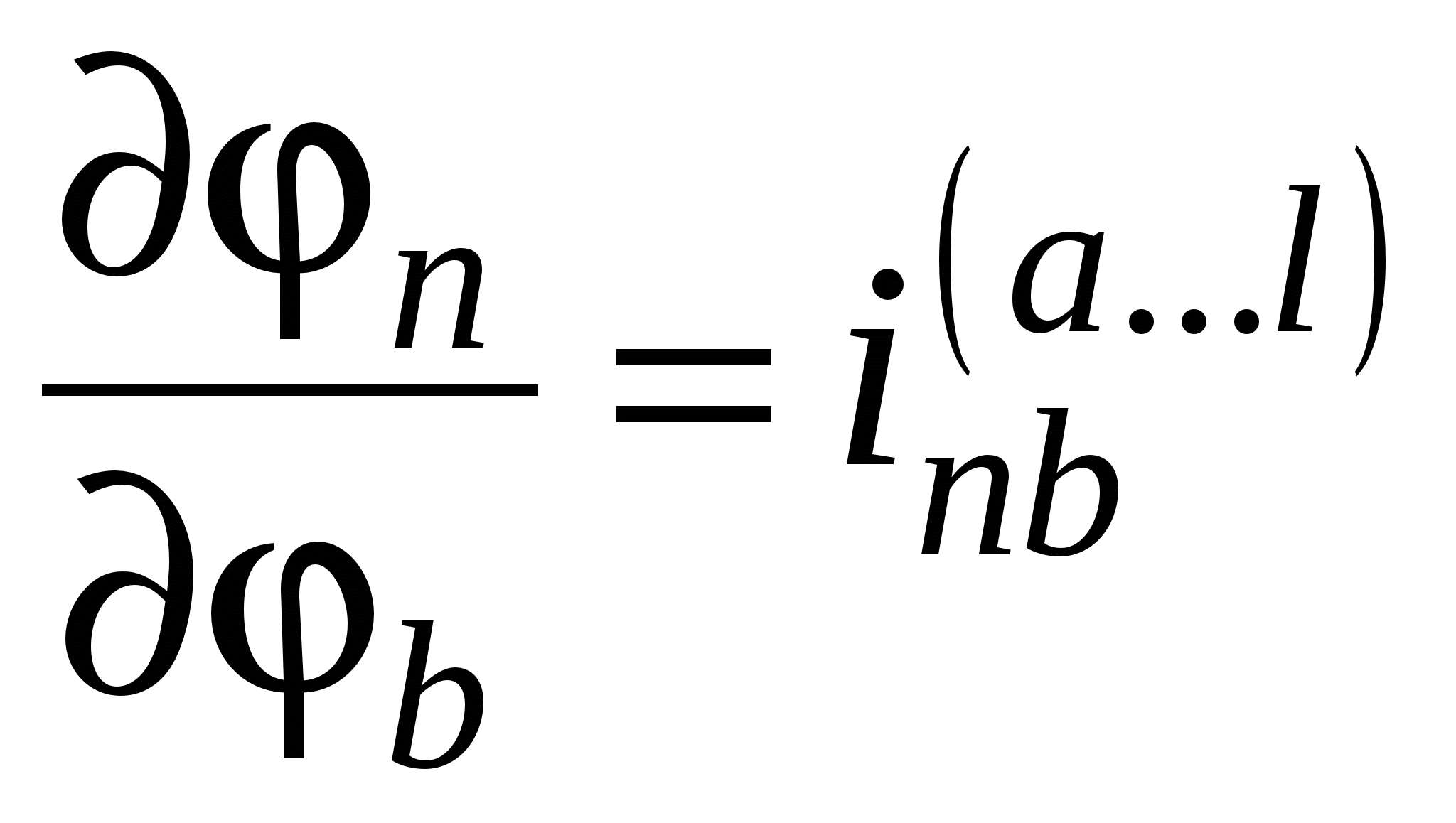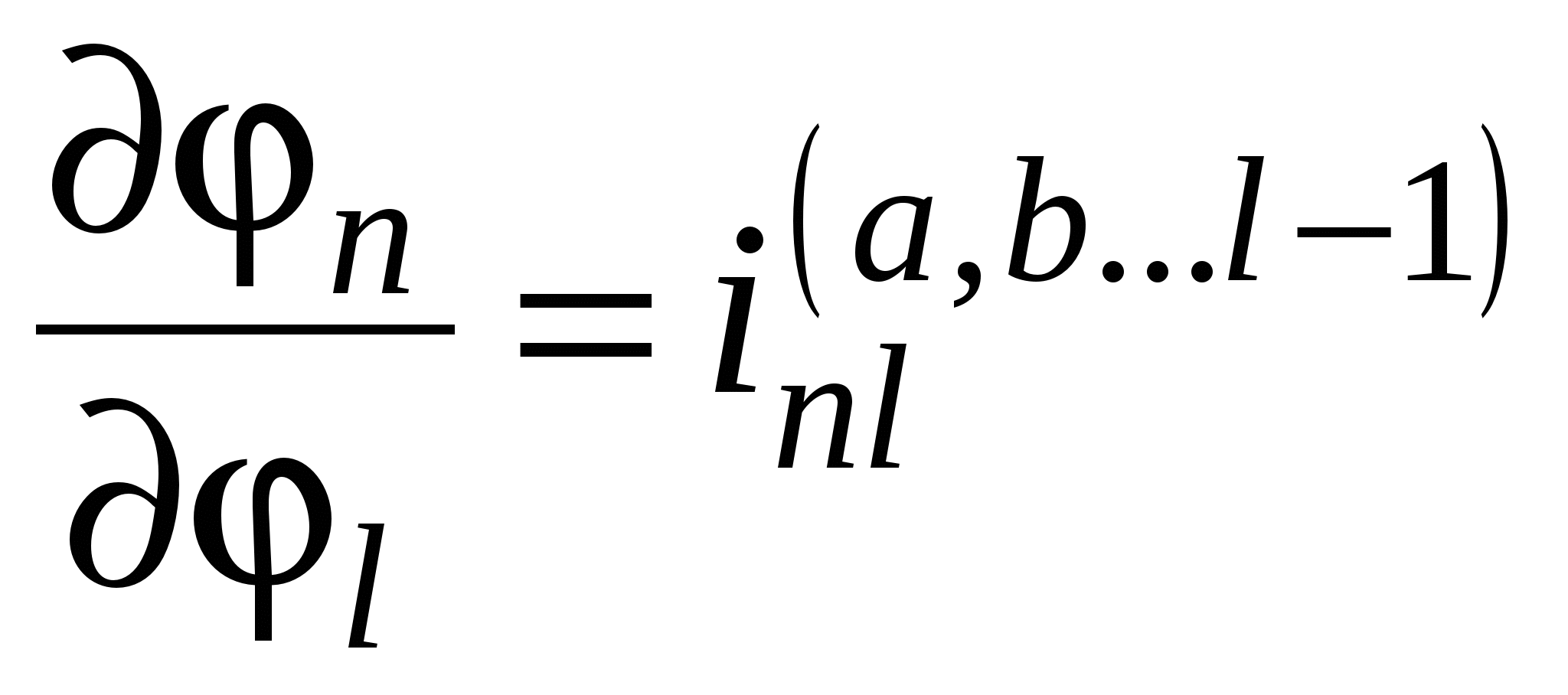Для дифференциала с двумя степенями свободы зависимость угловых скоростей имеет вид:
. (8)
Вывод: угловая скорость выходного звена дифференциала равна сумме угловых скоростей входных звеньев, умноженных на передаточные отношения от рассматриваемого выходного до соответствующего входного звена в предположении, что другие входные звенья остановлены.
В замкнутом дифференциале независимым движением обладает одно звено. Другие звенья кинематически связаны, поэтому можно выразить их углы поворота через угол поворота одного из звеньев, например, через ω а :
,
.
Подставив эти выражения в зависимость для ω п , получим:
Поделив обе части равенства на ω а , найдем передаточное отношение i па :
Для замкнутого дифференциала с тремя центральными звеньями п , а , в выражение примет вид
. (10)
Эта зависимость сразу получается из выражения для угловой скорости звена п дифференциала с двумя степенями свободы, если поделить обе части равенства на ω а .
Передаточное отношение замкнутого дифференциала можно вычислить, используя зависимость для незамкнутого дифференциала. Разрывом замыкающих цепей замкнутый дифференциал сводится к незамкнутому и определяются передаточные отношения
.
Затем в соответствии со схемами замыкающих цепей находятся их передаточные отношения
.
В другом способе определения передаточного отношения замкнутого дифференциала используется формула Виллиса для дифференциалов
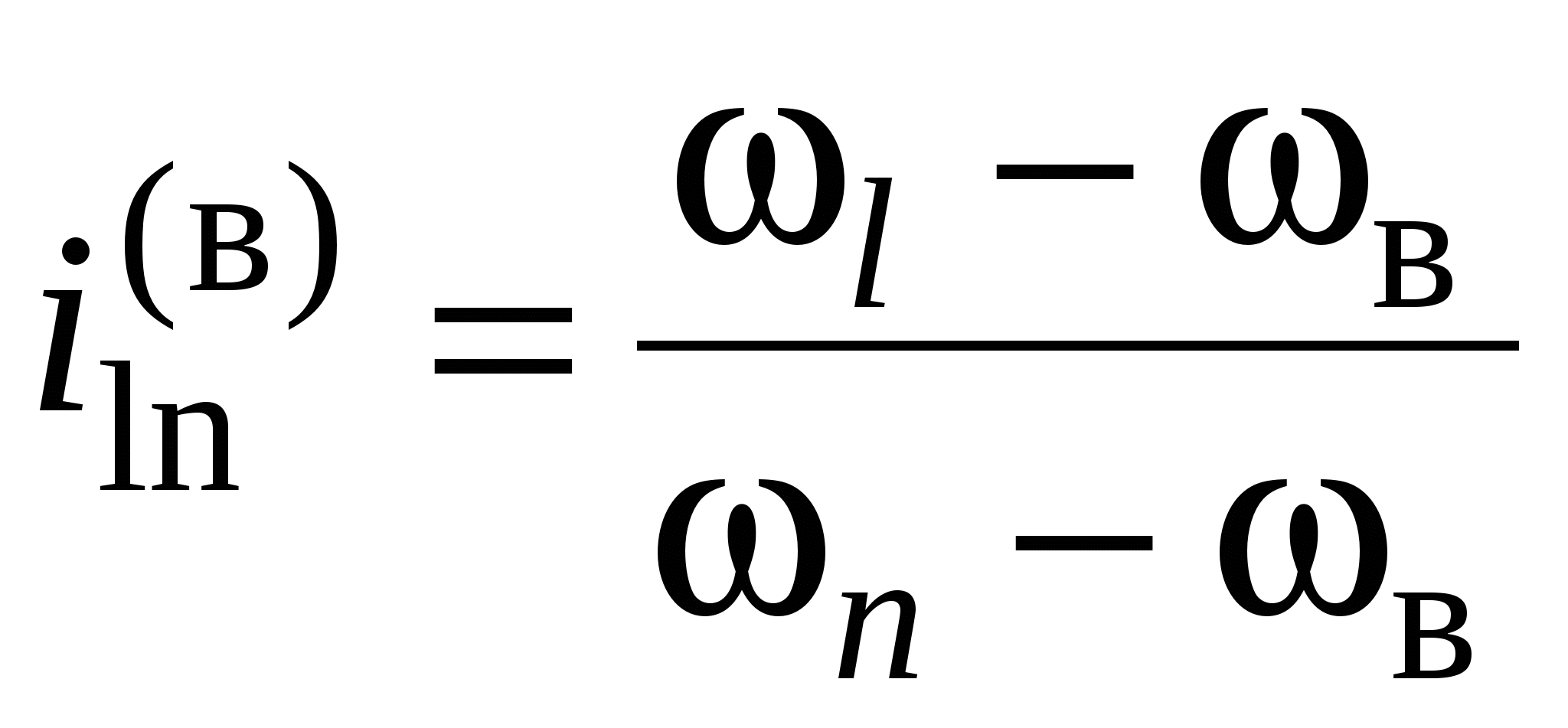. (11)
Замыкание возможно между одной из пар звеньев: l в, п в, l п.
Если замыкание осуществляется между звеньями l
и в, а требуется найти передаточное отношение от звена п
к звену в,
тогда, поделив числитель и знаменатель на ω b
(чтобы иметь требуемое передаточное отношение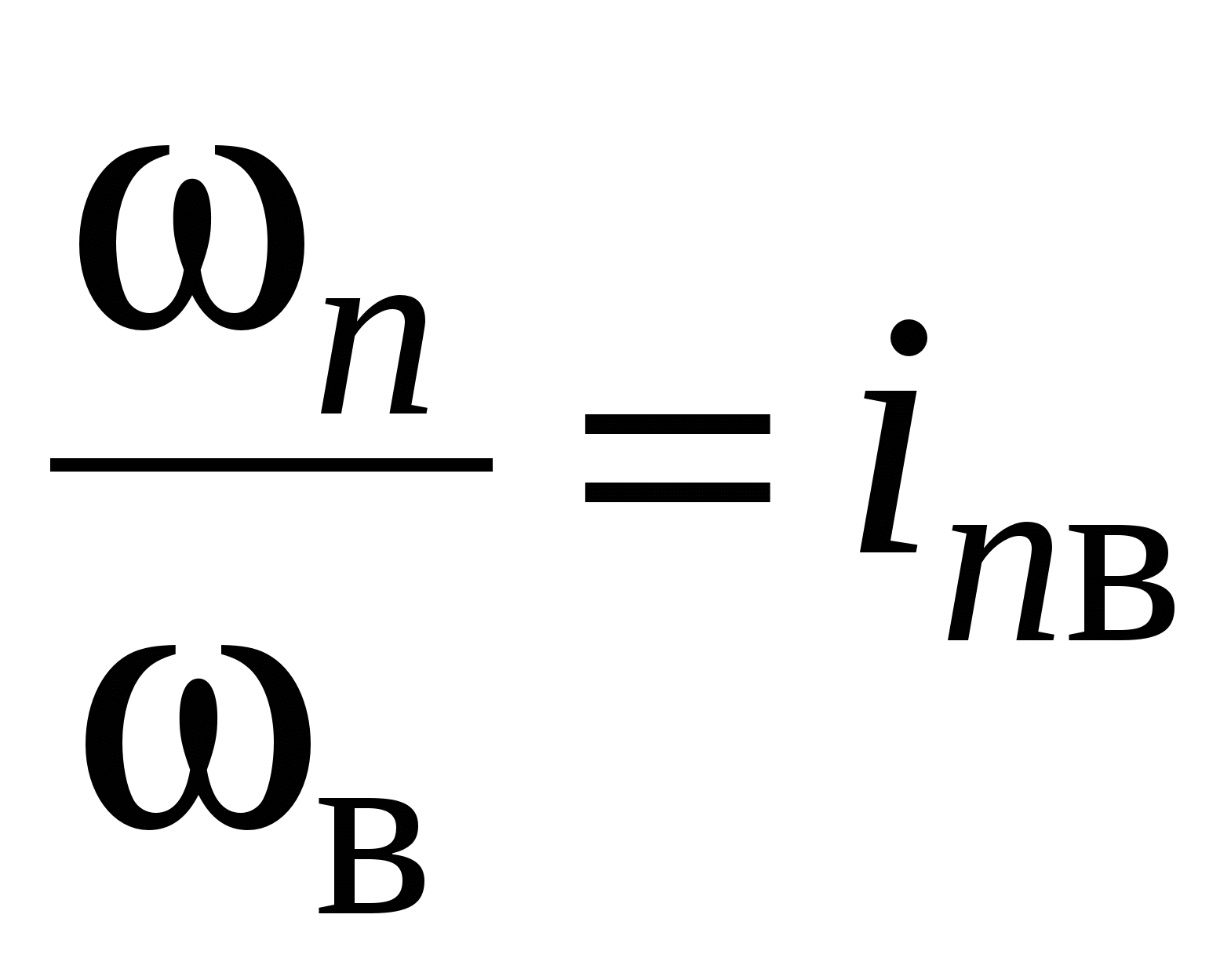 
,
получим:
,
где i
l
в
– передаточное отношение замыкающей цепи, определяется в соответствии со схемой замыкания; 
– передаточное отношение от звена l
к звену п
при остановленном водиле, определяется через числа зубьев механизма:
.
Пример
Найти передаточное отношение 
от водила к зубчатому колесу 4 и построить планы линейных и угловых скоростей планетарного механизма, изображенного на рис.8, где Z
1 = 30, Z
2 = 46, = 28, Z
3 = 104, = 20, Z
4 = 78, т =
2, ω в
= 5 с -1 .
Общее передаточное отношение 
необходимо разбить на два: передаточное отношение планетарного механизма 
, который составляют зубчатые колеса Z
1 , Z
2 , , Z
3 и водило В
и передаточное отношение простого зубчатого механизма i
34 , состоящего из колес Z
3 и Z
4 , так как формула Виллиса справедлива лишь для планетарных и дифференциальных механизмов:
.
Используя формулу Виллиса выразим передаточное отношение планетарного механизма 
через передаточное отношение обращенного механизма:
.
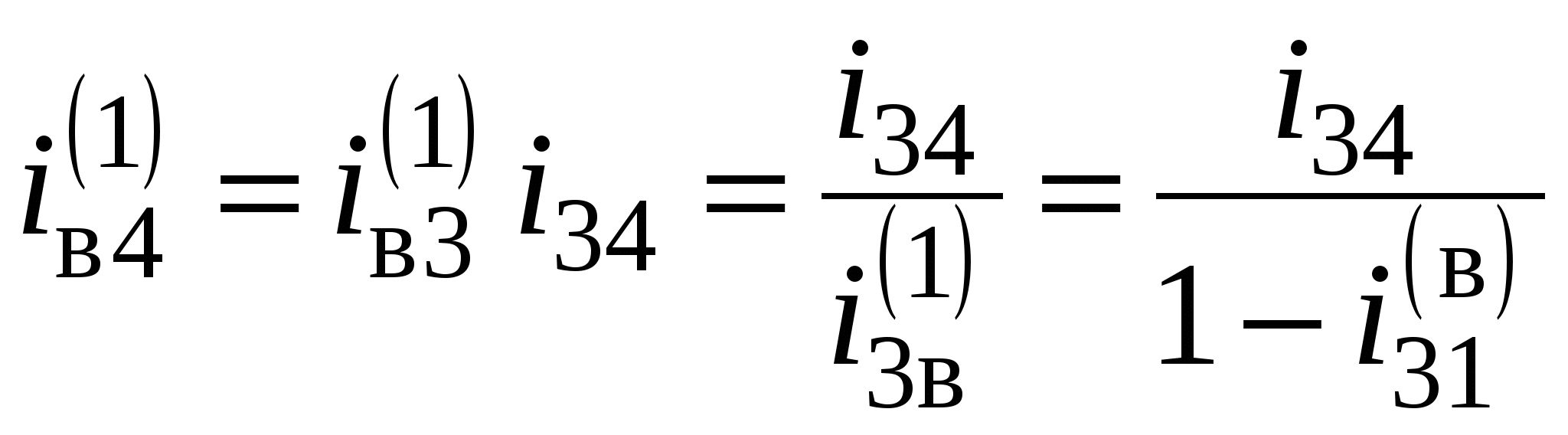Найдем передаточное отношение механизма с остановленным водилом 
:
.
Передаточное отношение простой зубчатой передачи
.
Искомое передаточное отношение
.
4. ПОСТРОЕНИЕ ПЛАНА ЛИНЕЙНЫХ СКОРОСТЕЙ
Построение плана возможно, если у каждого звена будут известны скорости минимум двух его точек. Прямая, соединяющая концы векторов скоростей этих точек – линия распределения скоростей звена, которому эти точки принадлежат.
Известными являются скорости точек звеньев, движение которых задано, а так же скорости точек неподвижных геометрических осей вращения звеньев (они равны нулю). При построении плана используется свойство эвольвентного зацепления: скорость полюса зацепления (мгновенного центра относительных скоростей) является общей для точек начальных окружностей зацепляющихся колес.
Обычно построение плана начинают со звена, скорость которого известна. В дифференциалах не всегда возможно построить план скоростей, начиная с входных звеньев. В таком случае построение начинают с любого другого звена, произвольно задавшись его скоростью. Получив план в произвольном масштабе, находят его действительный масштаб по известной скорости входных звеньев и соответствующему вектору-отрезку плана скоростей.
До построения плана скоростей должен быть изображен план механизма в определенном масштабе. Обычно известны размеры зубчатых колес (для плана необходимы диаметры их начальных окружностей d w ).
При несмещенной передаче диаметры начальных и делительных окружностей равны d w = d = mZ .
Масштаб плана механизма
(мм/мм),
где т ; Z – модуль и число зубьев колеса; l d – отрезок, изображающий диаметр начальной окружности зубчатого колеса.
Если рассматривается смещенное зацепление, то диаметры начальных окружностей определяются по формуле
,
где w – угол зацепления смещенной передачи; = 20º – стандартный угол зацепления.
При неизвестном значении модуля можно построить план механизма в масштабе чисел зубьев μ Z :
(мм -1)
Связь между масштабами μ l и μ Z : μ l = μ Z т.
Масштаб плана скоростей μ V определяется как отношение действительной скорости какой-либо точки механизма к длине вектора-отрезка, изображающего эту скорость на плане:
Если известны только числа зубьев колес механизма (неизвестны модули и угловые скорости), тогда план скоростей строится в произвольном масштабе. Скорость одной из точек механизма (обычно полюса зацепления какой-либо пары колес) изображается вектором-отрезком произвольной длины. Величины относительных скоростей зависят от размера выбранного вектора-отрезка, а отношение скоростей не зависит.
5. ПРИМЕР ПОСТРОЕНИЯ ПЛАНА ЛИНЕЙНЫХ СКОРОСТЕЙ
ПЛАНЕТАРНОГО МЕХАНИЗМА (рис.8)
Прежде всего строится план механизма в масштабе μ l :
мм/мм.
Масштаб μ Z равен:
мм -1 .
Найдем масштаб плана скоростей μ V
, произвольно задавшись вектором-отрезком скорости точки F
(
мм):
Теперь можно определить скорости всех точек звена 2
– блока сателлитов, так как известны скорости двух его точек А
и F
. Точка А
– полюс зацепления колес Z
1 и Z
2 , а поскольку колесо Z
1 неподвижно, то скорость точки А
равна нулю. Следовательно, распределение скоростей звена 2
изобразиться прямой, проходящей через точки а
и f
плана скоростей. На этой прямой находится точка «С
» – конец вектора 
, изображающего скорость точки С
– полюса зацепления колес и Z
3 .Теперь у звена 3
оказываются известными скорости двух точек: точки С
и геометрической оси вращения, которая равна нулю (на плане ей соответствует точка О
). Соединив точки «О
» и «С
» плана скоростей, получаем линию распределения скоростей звена 3
. Зубчатое колесо составляет одно целое со звеном 3
, поэтому скорость точки D
на плане скоростей изображается соответствующим вектором 
(точка d
находится на линии ОС
). Скорости точек звена 4
располагаются на отрезке прямой, проходящей через точки d
и О
4 , поскольку точка D
– полюс зацепления колес и Z
4 , а неподвижной геометрической оси колеса Z
4 соответствует точка О
4 плана скоростей к оси у-у
.
Углы наклона линий распределения скоростей к оси у-у пропорциональны угловым скоростям соответствующих звеньев, так как угловые скорости зубчатых колес с неподвижными геометрическими осями равны отношениям линейных скоростей точек начальных окружностей к радиусам начальных окружностей. Например, угловая скорость зубчатого колеса Z 3:
.
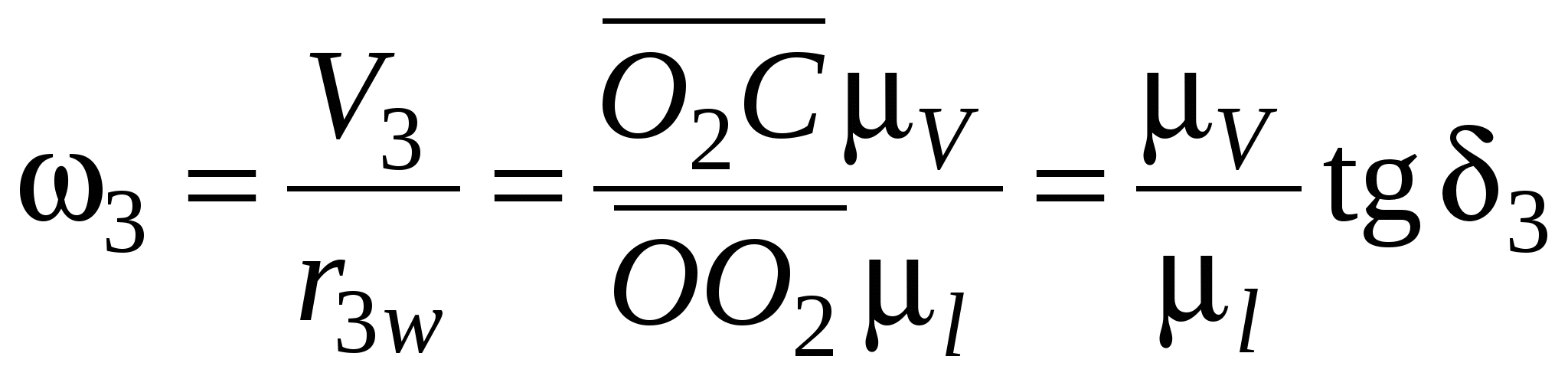В общем случае
. (13)
6. ПОСТРОЕНИЕ ПЛАНА УГЛОВЫХ СКОРОСТЕЙ
Построение плана угловых скоростей заключается в определении отрезков, пропорциональных углам наклона линий распределения скоростей к оси у-у – 
, и масштаба μ , в котором эти отрезки представляют угловые скорости звеньев.
Проводится горизонтальная прямая и перпендикулярно ей откладывается отрезок произвольной величины 
(рис.9). От величины отрезка зависит масштаб плана. Затем из конца отрезка – точки О
проводят лучи под углами δ i
к нему (параллельные линиям распределения скоростей звеньев). На горизонтальной прямой отсекаются отрезки 
пропорциональные углам δ i
, т.е. изображающие в неизвестном масштабе μ
угловые скорости ω i
звеньев механизма. Остается лишь определить масштаб плана μ .
Рис.9. План угловых скоростей планетарного механизма
Истинную величину угловой скорости ω i
уже нашли 
. Отрезок
на плане угловых скоростей, умноженный на масштаб плана μ
дает истинную величину угловой скорости, т.е.
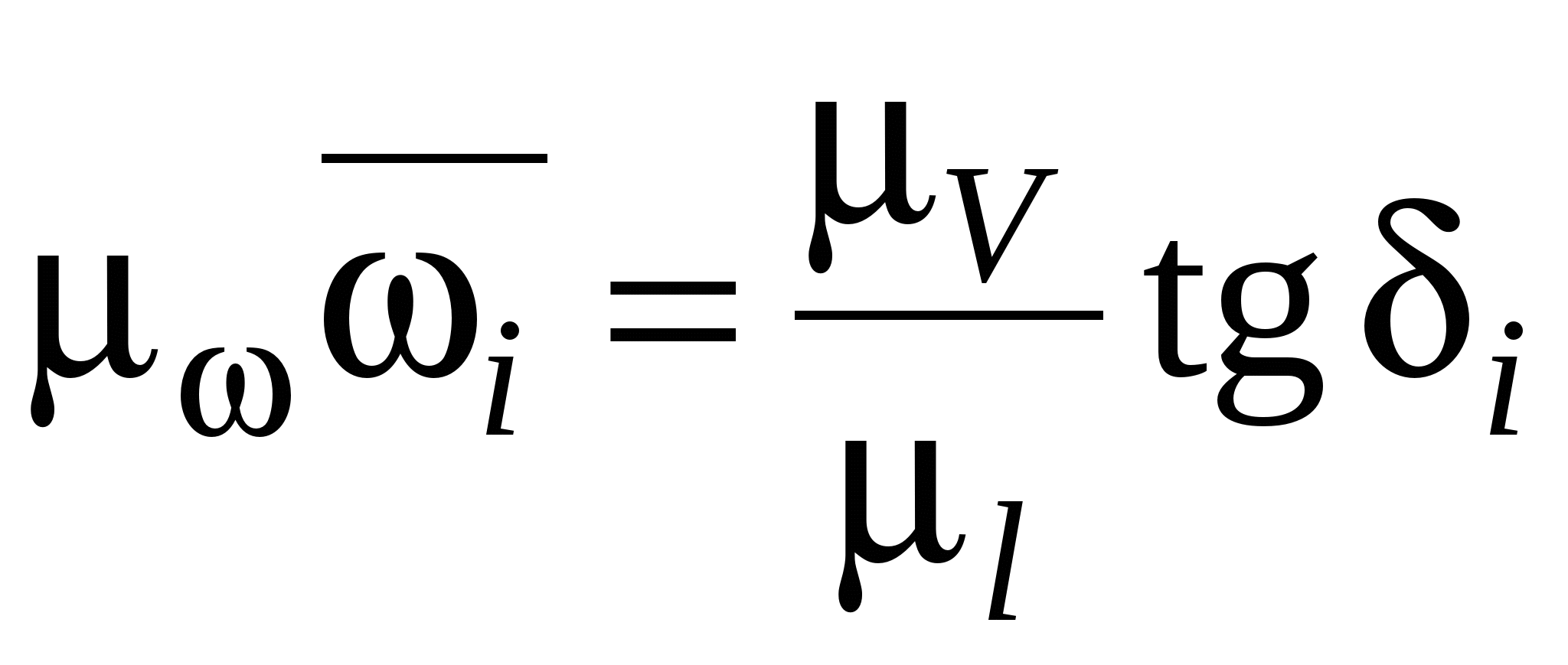, но 
, поэтому 
.
По отношению отрезков может быть определено передаточное отношение между звеньями механизма. Например, передаточное отношение от звена В к звену 4
.
Погрешность определения передаточного отношения графическим методом относительно аналитического метода:
Пример 2
Определить аналитически и графически угловую скорость звена 4 – ω 4 в зависимости от угловых скоростей звеньев 1 и В (ω 1 и ω в) для дифференциального механизма, изображенного на рис.10, и построить план линейных скоростей, если ω 1 = 10 с -1 , ω в = 5 с -1 .
Рис.10. Схема и план скоростей дифференциального механизма
Используя полученную зависимость угловых скоростей дифференциального механизма, для рассматриваемого приема будем иметь:
Отделяем простой зубчатый механизм от дифференциала.
Определим передаточные отношения:
1. простой зубчатой передачи:
;
2. обращенного механизма:
;
3. передаточное отношение планетарного механизма:
Подставив в выражение для ω 4 заданные и полученные величины, определим угловую скорость звена 4 :
Найдем ω 4 графически по плану линейных скоростей (рис.10):
.
с -1 .
Относительная погрешность определения угловой скорости ω 4
.
Пример 3
Определить аналитически и графически передаточное отношение от звена 1 к водилу В – i 1в замкнутого дифференциала (рис.11) и построить план линейных скоростей. Числа зубьев известны: Z 1 = 30, Z 2 = 46, = 28, Z 3 = 104, = 20, Z 4 = 78, Z 5 = 176.
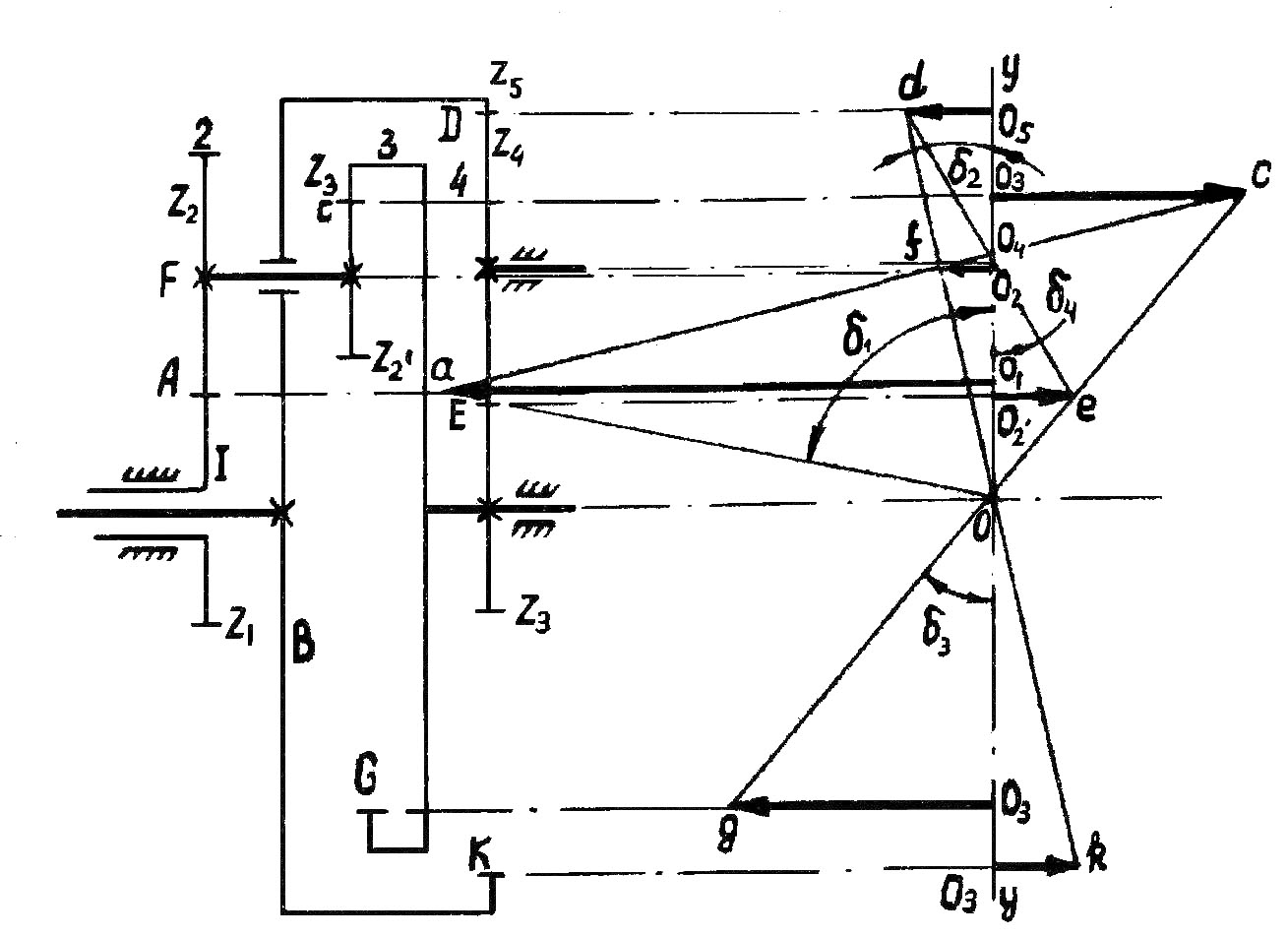
Рис.11. Схема и план скоростей замкнутого дифференциального механизма
Определим i 1в аналитически, используя зависимость угловых скоростей для замкнутого дифференциала. Уберем замыкающее звено – зубчатое колесо Z 5 , тогда получим механизм, изображенный на рис.10, для которого угловая скорость звена 1 определяется следующим выражением:
.
Найдем 
. При неподвижном звене 4
неподвижно и звено 3
, поэтому:
Определим 
:
Поделив обе части выражения для ω 1 на ω в, получим:
.
Вычислим передаточное отношение замыкающих цепей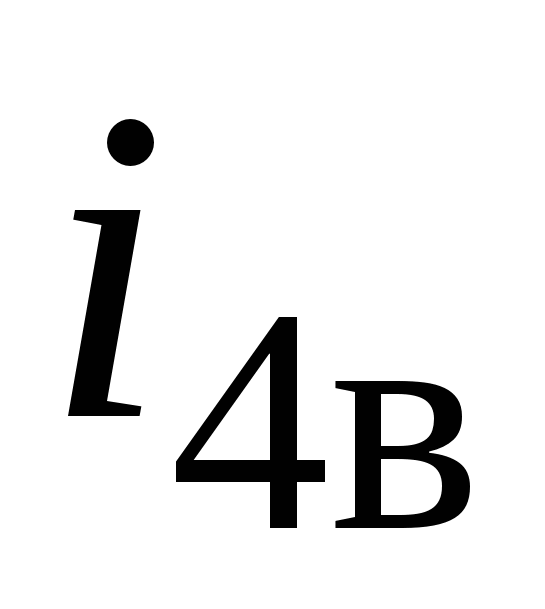 
:
.
Найдем искомое передаточное отношение 
2. Определим i 1в аналитически, используя формулу Виллиса для дифференциалов.
Запишем выражение для передаточного отношения от звена 1 к звену 4 :
где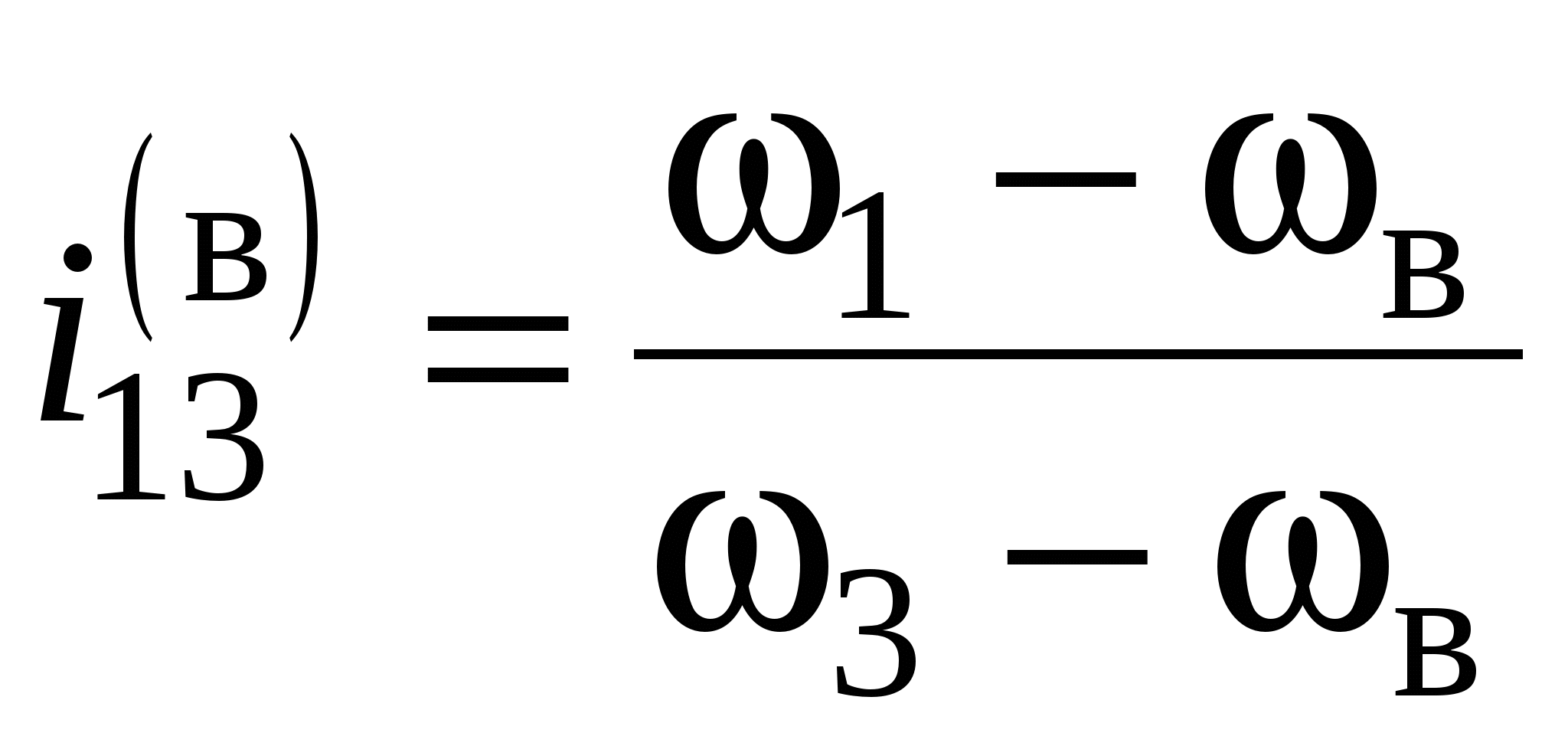 
.
Разделим числитель и знаменатель на ω в, чтобы получить искомое передаточное отношение i 1в:
,
откуда
.
Вычислим 
:
.
Определим передаточное отношение замыкающей цепи i 3в:
.
Найдем i 1в:
3. Определим i 1в графически
Построим план линейных скоростей механизма, который для рассматриваемого замкнутого дифференциала имеет такую особенность: план нельзя построить, начиная с ведущего звена 1 , так как для звена 2 оказывается известной лишь скорость одной точки А – полюса зацепления колес 1 и 2 . Поэтому построение начинают со звена 4 , произвольно задавшись его скоростью. По известным скоростям точек D
и оси вращения звена 4
, которая равна нулю (точка О
4 на плане скоростей), находим линию распределения скоростей звена 4
– 
. Затем строится линия распределения скоростей звена 3
, связанного со звеном С
и F
находится линия распределения скоростей звена 2
– 
и, следовательно, вектор скорости точки А
как полюса зацепления колес Z
2 и Z
1 . По известной скорости звена 1
определяется масштаб плана скоростей делением скорости точки А
на длину вектора-отрезка, изображающего эту скорость, 
.Передаточное отношение i 1в определяется по углам δ 1 и δ в плана скоростей:
.
Погрешность определения передаточного отношения i 1в аналитическим и графическим методами:
.
7. СИНТЕЗ ПЛАНЕТАРНОГО МЕХАНИЗМА
Синтез планетарного механизма заключается в подборе числа зубьев его колес таким образом, чтобы удовлетворить следующим условиям:
заданному передаточному отношению;
условию соосности;
условию соседства;
условию сборки;
условию правильного зацепления.
Условию соосности требует, чтобы при совпадении осей центральных колес и водила обеспечивалось зацепление сателлитов с центральными колесами.
Условие соседства требует, чтобы между окружностями выступов зубьев соседних сателлитов существовал зазор.
Для соблюдения этого условия требуется удовлетворить следующим неравенствам:
– (14)
при внешнем зацеплении сателлитов с центральным колесом (рис.13),
– (15)
при внутреннем зацеплении сателлитов с центральным колесом (рис.14), где К – число сателлитов.
Условие сборки – условие равных углов между сателлитами – требует одновременного зацепления всех сателлитов с центральными колесами при симметричном расположении зон зацепления.
Определим теоретически возможное число сателлитов, которое зависит от схемы механизма. Например, для механизма, изображенного на рис.12, при повороте центрального колеса 1
(и неподвижном колесе 3
) на угол равный шагу зубьев 
, водило повернется на угол 
.
Теоретически возможное число сателлитов, не совпадающих по положению:
;
.
Если сателлиты поставлены через l
зубьев центрального колеса в одной плоскости, то возможное их число 
(К
, п,
l
должны быть целыми числами).
Число сателлитов К определяется из условия соседства, поэтому условие сборки сводится к проверке, будет ли целым число l .
Условие правильного зацепления – условие отсутствия заклинивания и отсутствия интерференции зубьев. Числа зубьев зацепляющихся колес должны удовлетворять условиям, указанным в табл.1, соответствующей колесам, нарезанным долбяком.
Существует несколько методов подбора чисел зубьев планетарных передач. Рассмотрим наиболее простой из них, в котором подбор производится по двум условиям – заданному передаточному отношению и условию соосности. Затем выполняется проверка по трем следующим условиям: сборки, соседства, правильного зацепления.
Таблица 1
Условия правильного зацепления
| Внешнее зацепление | Внутреннее зацепление |
||||
| Z 1 | Z 2 | Z 1 | Z 2 | Z 1 | Z 2 |
| 13 | ≤17 | 17 | ∞ | 23 | ≥41 |
| 14 | ≤27 | 18 | ≥144 | 24 | ≥38 |
| 15 | ≤48 | 19 | ≥81 | 25 | ≥36 |
| 16 | ≤122 | 20 | ≥60 | 26 | ≥35 |
| 17 и | Любое | 21 | ≥50 | 27-79 | ≥Z 1 +8 |
| выше | 22 | ≥44 | 80 и выше | ≥Z 1 +7 |
|
Пример
Подобрать числа зубьев колес планетарного механизма, изображенного на рис.12, чтобы обеспечить передаточное отношение от первого звена к водилу равное 15 (
= 15).
Для заданной схемы выражение передаточного отношения имеет вид
.
Условие соосности при одинаковом модуле зубчатых колес выражается следующим образом:
Z 1 + Z 2 = Z 4 – Z 3 .
Из схемы ясно, что Z
4 должно быть больше Z
3 . Соотношение 
заменяем отношением сомножителей а, в, с, д, каждый из которых соответственно пропорционален числу зубьев, то есть а ~ Z
1 , в ~ Z
2 , с ~ Z
3 , д ~ Z
4:
.
Условие соосности: а + в = д – с.
Чтобы это условие выполнялось в любом случае, умножим правую часть равенства на левую, а левую – на правую:
(а + в) (д – с) = (д – с) (а + в).
Так как сомножители а, в, с, д пропорциональны числам зубьев, то для определения последних требуется умножить каждый сомножитель на коэффициент пропорциональности γ. Очевидно, что γ – любое положительное число. Таким образом получим:
γ(а +) (д –) = γ(д – с) (а + в).
Преобразуем неравенство к виду:
а(д – с) γ + в(д – с) γ = д(а +в) γ – с(а +в) γ.
Теперь можно принять что:
Z 1 = а(д – с) γ, Z 2 = в(д – с) γ, Z 3 = с(а +в) γ, Z 4 = д(а +в) γ.
Разобьем передаточное отношение = 14 на четыре сомножителя, которые должны быть целыми числами. Это можно выполнить следующим образом:
и т.п.
Рассмотрим первый вариант: а = 1, в = 2, с = 1, д = 7. Решение ищем в ранее полученном виде:
Z 1 = а (д – с) γ = 1 6 γ = 6γ;
Z 2 = в (д – с) γ = 2 6 γ = 12γ;
Z 3 = с (а + в) γ = 1 3 γ = 3γ;
Z 4 = д (а + в) γ = 7 3 γ = 21γ.
Можно разделить правые части на 3, тогда Z 1 = 2γ, Z 2 = 4γ, Z 3 = γ, Z 4 = 7γ. Наименьшим должно быть зубчатое колесо Z 3 . Число зубьев колеса Z 3 определяется из условия отсутствия интерференции зубьев при зацеплении с колесом Z 4 ; Z 3 должно быть более 17, так как при 17 зубьях правильное зацепление возможно лишь с зубчатой рейкой. При Z 3 = 18, Z 4 = 7Z 3 = 7 18 = 126. Согласно табл.1 при 18 зубьях колеса Z 3 , Z 4 должно быть более 144, т.е. условие правильного внутреннего зацепления не удовлетворяется. Принимаем Z 3 = 19 тогда Z 4 = 133, для обеспечения правильного зацепления Z 4 , согласно табл.1, должно быть более 81. То есть теперь соблюдаются условия правильного зацепления в обоих случаях – при внешнем и при внутреннем зацеплении зубчатых колес планетарного механизма, поскольку числа зубьев колес 1 и 2 равны: Z 1 = 38, Z 2 = 76, так как Z 3 = γ, Z 1 = 2γ, Z 2 = 4γ.
Найдем возможное число сателлитов по внешнему зацеплению:
.
По внутреннему зацеплению:
.
Проверим условие сборки при четных сателлитах:
Условие сборки не удовлетворяется, поэтому возьмем три сателлита и снова проверим условие сборки:
.
Теперь условие сборки обеспечивается.
Рассмотрим четвертый вариант разбивки передаточного отношения:
; а = 1, в = 4, с = 2, д = 7.
Числа зубьев ищем в виде:
Z 1 = а (д – с) γ = 1 5 γ = 5γ;
Z 2 = в (д – с) γ = 4 5 γ = 20γ;
Z 3 = с (а + в) γ = 2 5 γ = 10γ;
Z 4 = д (а + в) γ = 7 5 γ = 35γ.
Примем Z 1 = 18, тогда Z 2 = 72, Z 3 = 36, Z 4 = 126 зубьев.
Условия правильного зацепления выполняются, так как для внешнего зацепления исходили из этого условия, приняв Z 1 > 17. Правильность внутреннего зацепления обеспечивается, поскольку при Z 3 = 36, согласно табл.1, Z 4 > Z 3 + 8. У нас Z 4 = 126; 126 > 36 + 8.
Определим возможное число сателлитов по внешнему зацеплению:
.
По внутреннему зацеплению:
.
Число сателлитов может быть не более трех. Проверим условие сборки при трех сателлитах:
.
Условие сборки выполняется.
Сравнивая два рассмотренных варианта, находим, что во втором случае габариты редуктора получаются меньшими.
ЛИТЕРАТУРА
Гуслякова Г.П., Воробьева И.В. Зубчатые цилиндрические передачи. Основы теории и проектного анализа: Учеб. пособие / НГТУ. – Н.Новгород. 2003. – 132 с.
Попов С.А., Тимофеев Г.А. Курсовое проектирование по теории механизмов и механике машин: Учеб. пособие для втузов / Под ред. К.В.Фролова. – М.: Высш. шк., 2002. – 411 с.
Теория механизмов и машин: Учеб. для вузов / Фролов К.В., Попов С.А., Мусатов А.К. и др.; Под ред. К.В.Фролова. – М.: Высш. шк., 2003. – 496 с.
Центральное колесо 1 называется солнечным, а неподвижное 3 - коронным или корончатым. Зубчатое колесо 2 имеющее подвижную ось называется сателлитом. Звено Н называется водилом или поводком. Механизмы, в состав которых входят зубчатые колеса с подвижными осями называются планетарными или дифференциальными.
Планетарными (рис. 14 а) называются механизмы, имеющие одну степень свободы. Дифференциальные (рис. 14 б) механизмы имеют две и более степени свободы.
Эти механизмы обязательно должны быть соосными, то есть оси солнечных колёс должны располагаться на одной и той же прямой линии.
Рассмотрим дифференциальный механизм (рис. 15).
где: n=4; ; .
Таким образом определённость в движении звеньев этого механизма будет в том случае, если будут известны законы движения двух его ведущих звеньев.
Так как сателлиты имеют подвижные оси, то использовать формулы для расчёта передаточного отношения механизмов с неподвижными осями не представляется возможным. В этом случае прибегают к методу инверсии (метод обращённого движения).
Будем рассматривать движение всех колёс относительно водила. Всем звеньям зададим вращательное движение с угловой скоростью водила, но в обратном направлении и найдём скорости всех звеньев механизма. Для этого вычтем угловую скорость водила из всех угловых скоростей колёс.
|
|
Таблица 2.
| № Звеньев | Скорость звена в действительном движении (до инверсии) | Скорость звена в обращённом движении (после инверсии) |
|
|
||
|
|
||
| Колесо 2’ |
|
|
|
|
||
|
|
Механизм, полученный в результате инверсии (остановки водила) называется обращённым (рис. 16). В результате получили обычную зубчатую передачу с неподвижными осями.
|
|
Эту зависимость (1) называют формулой Виллиса для дифференциальных механизмов.
Если бы было n - колёс, то:
где s – солнечное колесо.
Дифференциальный механизм никакого определённого передаточного отношения не имеет, если ведущим является одно из звеньев (колесо или водило), и приобретает определённость, если ведущих колёс будет два.
